松高ライフ☆令和5年度

7月10日と12日の2日間にわたって23HR数学B選択者を対象に

単元「数列」における「問題づくり」をおこないました。

まずは「等比数列の和」を扱った原問題を解きます。

ワークシートはメタモジで共有され、お互いに見られるようになっています。

解き方が分からない場合は友達のワークシートをみて

解き方を確認したりすることができます。

解き方を確認し、単元の学習内容をふりかえります。

次に、かえられるところはないか考えます。

目標の1つに「日常生活の中から問題を発見する」ことがあります。

自分事に捉え、目的を持った問題にかえることができないか考えます。

原問題は15日間の貯金の総額を求める問題ですが、

先に目標金額を決め、その金額は何日後に貯まるかといった問題や、

陸上競技部の生徒が、自分の目標タイムを達成するのは何日後かといった問題

等比数列でなく等差数列で金額を増やしていったときの総額を求める問題

など、さまざまな問題づくりができました。

2時間目はつくった問題をグループで共有します。

他の人とつくった問題を共有し、相互評価をおこないます。

「オリジナリティ」「タイトル」「解答」の観点は与えられていますが、

それ以外でどんな観点が考えられるか、言語化していきます。

初めての活動でこの観点を考える場面が一番苦戦していたように思います。

苦戦しながらも、「現実的な問題か」「ユニーク」「身近な問題か」などの観点が挙げられていました。

最後に他者の意見を聞いて自分のつくった問題のレベルを少しでも上げることはできないか、改善していきます。

他者の意見を聞いて、改善を加えて模範解答も作成します。

最後のふりかえりでは

自分のつくった問題を解くことで、原問題も解けるようになった

自分が気になっていたことを解く機会を持つことができておもしろかった

など、問題づくりを通して思考力を働かせ、日常生活と結びつけることができました。

「難しかった」という感想が多かった中で、時間いっぱい問題づくりにチャレンジする姿が見られました。

７月10日（月）の４限目、生徒会役員が中心となって、校則について考え話し合うホームルーム活動をZOOM配信で行いました。

１．生徒会役員がZOOMを通して各ホームルームの生徒に本時の説明を行う。

　　・ルールやマナーについて

　　・校則の見直しについて

２．生徒会役員の指示に従って、各ホームルームでグループ分かれ、意見を出し合う。

　　・ホームルーム委員長は「松高の諸ルール等」をクラス全員に配布。

　　・ホームルーム副委員長は記入用紙を各グループに配布。

　　「変更したいルール等とその理由」、「削除したいルール等とその理由」、「追加したいルール等とその理由」

　　・委員長が司会を務め、グループ代表者が意見を発表、ホームルーム書記がそれをまとめる。

３．各ホームルームで生徒総会での要望事項（校則以外）を考える。

　　・生徒総会での要望事項についてホームルームで話し合う。

　　「提案の内容とその理由」

１年生の様子

２年生の様子

３年生の様子

生徒会役員によるZOOM配信

 なお、校則の見直しに関する今後の予定は以下の通りです。

ホームルーム活動で見直しを提案

　　　　　　↓

各ホームルーム代議員が見直し案について審議

　　　　　　↓

生徒総会で代表ホームルーム提案

　　　　　　↓

教職員との話し合い

3年理系クラスⅠAコースで単元「三角比」における「問題づくり」研究授業をおこないました。

この授業の目標は

①　三角比の単元の内容をふりかえること（知識及び技能）（自分とむきあう）

②　自分の日常生活の中から問題を発見し、学習内容を活用して解決すること（思考力・判断力・表現力等）（世界　　とむきあう）

③　他者の意見を聞いて自分の課題に生かすこと（学びに向かう力・人間性等）（人とむきあう）

の３つです。

各場面でこの目標を意識しながら取り組みました。

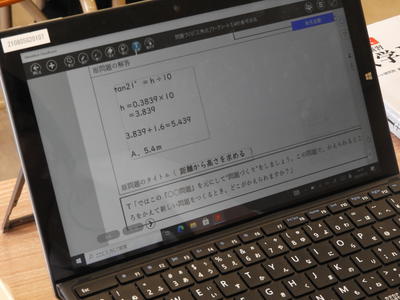
まず原問題を解決します。

ワークシートはメタモジで配布され、お互いに見られるようになっています。

21°のタンジェントを使うのでその値が必要ですが、

それぞれ参考書の三角比の表のページから必要な値を抜き出して使えていました。

この問題の目的を考えるため、解いた問題にタイトルをつけます。

それぞれのタイトルがつけられていました。

次にかえられるところはないか、考えていきます。

なぜその値にしたのか、何を求めたいのか考えながら問題づくりをおこないます。

次につくった問題を共有し、どこがよかったか観点を考え、評価ルーブリックをそれぞれが作成します。

「オリジナリティ」「タイトル」「解答」以外に「現実的な問題か」などの観点を見つけられた生徒がいました。

松高ルーブリックにあわせて、レベル１～３で評価していきます。

他者の意見を取り入れ、自分のつくった問題が少しでもレベルがあがるように

かえられるところはないか考え、仕上げていきます。

最終的に提出された問題には

高さの分かっているもの（富士山やスカイツリーなど）から

見上げた角度を求める問題、

対象物までの距離を求める問題、

2カ所の地点からの角度を利用して高さを求める問題

自分の家の高さを求める問題など、工夫がみられる問題がたくさんできました。

何より、生徒たちは主体的に取り組んでおり、学びの自走を感じられる授業となりました。

3年理系ⅠAコースで、切り紙の仕組みについて考えました。

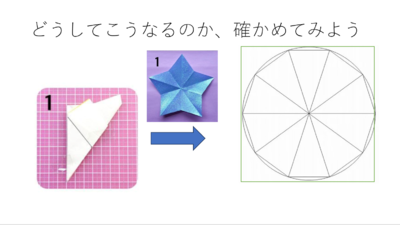
まず切り紙を体験します。

「十折り」という方法で折り紙を折ります。

線で切ったらどの形が現れるのかを考えます。

どうしてこの形が現れたのか、対称性を用いて確かめていきます。

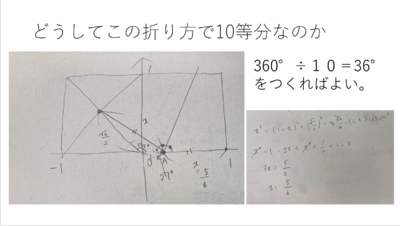
次に、この折り方で１０等分をつくることができたのか確かめていきます。

1辺の長さを２と仮定し、中点が原点となるようにｘの範囲を－１から１とし、余弦定理を用います。

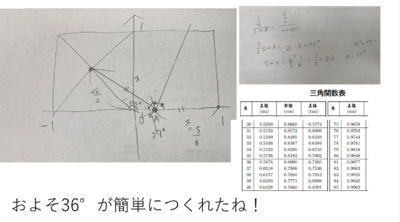
次に正弦定理を用いてサインの値を求め、三角比の表から36°（360°÷10）であることを確認します。

何気なくやっている折り紙にも数学で説明できる理論が潜んでいることが分かります。

次にこの十折りの対称性を活かして切り紙製作をしました。

日頃から問題づくりに取り組んできたからか、問題を発展させようとします。

星や花だけでなく、キャラクターが手をつないでつながった図案や

十折りでなく十六折りで考える、など問題を発展させて学びを楽しむことができました。

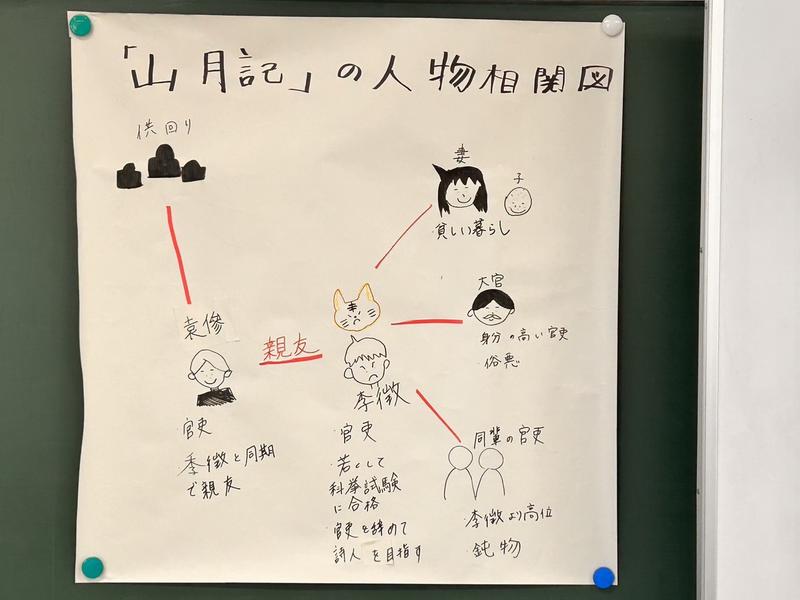
 ３年生の現代文の授業では、昨年の『こころ』に引き続き、中島敦の『山月記』を題材として生徒授業(本校のスクールミッション)を行いました。

授業では、最初に各班ごとに問いを立て、その問いについて話し合った後、次にそれをどのように他の生徒に伝えていくかについて協議･検討し、授業づくりを行いました。

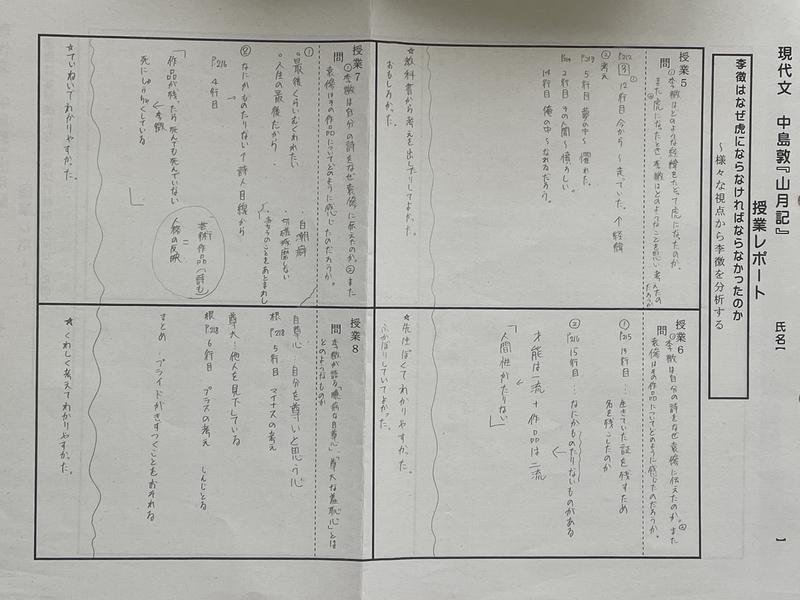
生徒授業では、パワーポイントや板書などを活用して、他の生徒に対して授業を行いました。他の生徒の授業を聞くことで、自分たちが気づけなかったことを知ることができ、深い学びにつなげることができました。

昨年よりも生徒たちの｢伝える力｣に大きな伸びが見られ、大変有意義な時間となりました。

〈生徒授業の様子〉

〈生徒が作成した教材の一例〉

〈生徒授業のノート〉